3. 파이토치로 구현하는 ANN
3.1 텐서와 Autograd
3.1.1 텐서의 차원 자유자재로 다루기
# 파이토치 import
import torch
텐서 = 숫자들을 일정한 모양으로 배열한 것 랭크 = 차원 랭크에 따른 형태
- 1 -> 스칼라 / 모양: []
- [1, 2, 3] -> 벡터 / 모양: [3]
- [[1, 2, 3]] -> 행렬 / 모양: [1, 3]
- [[[1, 2, 3]]] -> n랭크 텐서 / 모양: [1, 1, 3]
x = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print(x)
출력값
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
print(f"Size: {x.size()}")
print(f"Shape: {x.shape}")
print(f"랭크(차원): {x.ndimension()}")
출력값
Size: torch.Size([3, 3])
Shape: torch.Size([3, 3])
랭크(차원): 2
unsqueeze(), squeeze(), view() 함수로 텐서의 랭크와 shape를 인위적으로 바꿀 수 있다!
# 랭크 늘리기
x = torch.unsqueeze(x, 0)
print(x)
print(f"Size: {x.size()}")
print(f"Shape: {x.shape}")
print(f"랭크(차원): {x.ndimension()}")
출력값
tensor([[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]])
Size: torch.Size([1, 3, 3])
Shape: torch.Size([1, 3, 3])
랭크(차원): 3
[3, 3] 형태의 랭크 2 텐서의 첫 번째 자리에 1이라는 차원값을 추가하여 [1, 3, 3] 모양의 랭크 3 텐서로 변경.
# 랭크 줄이기
x = torch.squeeze(x)
print(x)
print(f"Size: {x.size()}")
print(f"Shape: {x.shape}")
print(f"랭크(차원): {x.ndimension()}")
출력값
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
Size: torch.Size([3, 3])
Shape: torch.Size([3, 3])
랭크(차원): 2
squeeze(), unsqueeze() 를 사용해서 차원 수를 늘리고 줄여도 총 원소 수는 유지되는 것을 확인할 수 있다!
view() : 원소 수 유지하면서 텐서 크기 변경.
# x를 [3, 3] -> [9]
x = x.view(9)
print(x)
print(f"Size: {x.size()}")
print(f"Shape: {x.shape}")
print(f"랭크(차원): {x.ndimension()}")
출력값
tensor([1, 2, 3, 4, 5, 6, 7, 8, 9])
Size: torch.Size([9])
Shape: torch.Size([9])
랭크(차원): 1
view() 예시를 하나만 더 살펴보자면,
ex = torch.tensor([[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [9, 10, 11]]])
print(f"Size: {ex.size()}")
print(f"Shape: {ex.shape}")
print(f"랭크(차원): {ex.ndimension()}")
출력값
Size: torch.Size([2, 2, 3])
Shape: torch.Size([2, 2, 3])
랭크(차원): 3
print(ex.view([-1, 3])) # ex라는 텐서를 (?, 3)의 크기로 변경
print(ex.view([-1, 3]).shape)
출력값
tensor([[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]])
torch.Size([4, 3])
3.1.2 텐서를 이용한 연산과 행렬곱
import torch
w = torch.randn(5, 3, dtype = torch.float)
x = torch.tensor([[1.0,2.0], [3.0, 4.0], [5.0, 6.0]])
print("w size: ", w.size()) # 5, 3
print("x size: ", x.size()) # 3, 2
print("w: ", w)
print("x: ", x)
출력값
w size: torch.Size([5, 3])
x size: torch.Size([3, 2])
w: tensor([[-0.2160, -0.1075, -0.4239],
[-1.3240, -1.0760, -1.1653],
[-1.6739, 0.9338, -0.4222],
[ 0.0161, -0.3775, -0.3342],
[ 1.5347, -0.6861, 1.4807]])
x: tensor([[1., 2.],
[3., 4.],
[5., 6.]])
b = torch.randn(5, 2, dtype = torch.float)
print("b size: ", b.size())
print("b: ", b)
출력값
b size: torch.Size([5, 2])
b: tensor([[-0.8994, -1.2410],
[ 0.3491, -0.0774],
[-0.8490, -0.2266],
[-0.5137, 0.0152],
[ 0.7142, -2.1923]])
# 행렬곱 구하기
wx = torch.mm(w, x)
print(f"wx: {wx}")
print(f"wx size: {wx.size()}")
출력값
wx: tensor([[ -2.6579, -3.4053],
[-10.3782, -13.9434],
[ -0.9836, -2.1459],
[ -2.7875, -3.4832],
[ 6.8798, 9.2090]])
wx size: torch.Size([5, 2])
# 행렬 덧셈
result = wx + b
print(f"result: {result}")
print(f"result size: {result.size()}")
출력값
result: tensor([[ -3.5574, -4.6463],
[-10.0291, -14.0208],
[ -1.8326, -2.3725],
[ -3.3012, -3.4680],
[ 7.5939, 7.0167]])
result size: torch.Size([5, 2])
3.1.3 Autograd
Autograd = 자동 기울기
- 거리(distance) = 정답과 머신러닝 모델이 예측한 결과의 차이
- 오차(loss) = 학습 데이터로 계산한 거리들의 평균
오차 최소화하는 알고리즘 중 가장 유명하고 많이 쓰이는 것 = 경사하강법
- 값이 1.0인 스칼라 텐서 w 정의 후, 수식 w에 대해 미분하여 기울기 계산하기
requires_grad = True로 설정하면 파이토치 Autograd 기능이 계산할 때 자동으로 w에 대한 미분값을 w.grad 에 저장함.
w = torch.tensor(1.0, requires_grad = True)
a = w * 3
l = a ** 2
현재 상황 : l = a**2 = (3w)**2 = 9 * (w**2)
l을 w로 미분하려면 연쇄법칙 사용해야함. -> backward() 함수 사용
📌 좀 더 알아보기
- requires_grad
- backward()
print((w.is_leaf == True) and (w.grad_fn == None))
print((a.is_leaf == True) and (a.grad_fn == None))
print((l.is_leaf == True) and (l.grad_fn == None))
print("---")
print(a.is_leaf)
print(a.grad_fn)
print("---")
print(l.is_leaf)
print(l.grad_fn)
출력값
True
False
False
---
False
<MulBackward0 object at 0x0000025F0EB40160>
---
False
<PowBackward0 object at 0x0000025F0EB43820>
- leaf 텐서 = 기존 연산 기록이 없는 텐서.
- w는 leaf 텐서이다. (w.is_leaf == True, w.grad_fn == None)
- a와 l은 leaf 텐서가 아니다.
어떤 연산을 했느냐에 따라 grad_fn에 AddBackward0, SubBackward0, MulBackward0, DivBackward0, PowBackward0 와 같이 저장되어 있는 것을 확인할 수 있다.
backward()는 leaf 텐서의 .grad, 즉 기울기를 계산한다.
이를 계산하기 위해서는 전제조건이 필요하다.
- 역미분을 수행하려는 하나 이상의 leaf 텐서가
requires_grad = True일 것 backward()를 호출하는 텐서는 스칼라일 것.- 미분 가능한 연산일 것. (미분 불가능한 연산 또는 점의 grad는 계산 결과를 신뢰할 수 없다.)
l.backward()
print(f"l을 w로 미분한 값은 {w.grad}")
출력값
l을 w로 미분한 값은 18.0
backward()를 실행하면 .grad_fn에 기록된 정보를 시작으로 마지막 연산부터 거슬러 올라가며 역미분을 수행한다.
| leaf 텐서 | non-leaf 텐서 | |
|---|---|---|
| is_leaf | True | False |
| grad | 존재 | None |
| grad_fn | None | 존재 |
이 때 backward 경로 상에 있는 non-leaf 텐서는 leaf 텐서의 grad 를 계산하기 위해 항상 requires_grad = True 여야한다.
3.2 경사하강법으로 이미지 복원하기
3.2.1 오염된 이미지 문제
이미지 처리를 위해 만들어 두었던 weird_function() 함수에 실수로 버그가 들어가 100x100 픽셀의 오염된 이미지가 만들어졌다. 오염된 이미지와 weird_function() 함수를 활용해 원본 이미지를 복원하자.
3.2.2 오염된 이미지를 복원하는 방법
weird_function()을 살펴보고 반대로 동작하는 함수를 구현하는 것도 방법일 수 있지만, 함수 하나하나 뜯어보는건 너무 까다로운 작업.
-> 크기 같은 랜덤 텐서 생성하고 얘를 weird_function()에 넣었을 때, 결과(=가설)가 오염된 이미지와 같다면, 랜덤 텐서 = 원본 이미지가 된다!
3.2.3 문제 해결과 코드 구현
import torch
import pickle
import matplotlib.pyplot as plt
img_path = "3-min-pytorch/03-파이토치로_구현하는_ANN"
# 오염된 이미지 불러오기
broken_image = torch.FloatTensor( pickle.load(open(img_path + "/broken_image_t.p", "rb"), encoding = "latin1" ) )
# 오염된 이미지 출력하여 확인
plt.imshow(broken_image.view(100, 100))

# weird_function
def weird_function(x, n_iter=5):
h = x
filt = torch.tensor([-1./3, 1./3, -1./3])
for i in range(n_iter):
zero_tensor = torch.tensor([1.0*0])
h_l = torch.cat( (zero_tensor, h[:-1]), 0)
h_r = torch.cat((h[1:], zero_tensor), 0 )
h = filt[0] * h + filt[2] * h_l + filt[1] * h_r
if i % 2 == 0:
h = torch.cat( (h[h.shape[0]//2:],h[:h.shape[0]//2]), 0 )
return h
코드를 이해하여 반대로 실행하지 않고, 머신러닝을 이용하여 이미지를 복원해보자
# 무작위 텐서를 weird_function 함수에 입력해 얻은 가설 텐서와
# 오염된 이미지 사이의 오차 구하는 함수 구현
def distance_loss(h, broken_image):
return torch.dist(h, broken_image)
torch.dist() : 두 텐서 사이의 거리 구하는 함수
# 오염된 이미지와 크기가 같은 랜덤 텐서 생성하기
random_tensor = torch.randn(100*100, dtype = torch.float)
경사하강법은 여러 번 반복해서 이루어짐. 한 반복에서 최솟점으로 얼마나 많이 이동하는지를 정하는 매개변수를 학습률이라고 한다. 우선 0.8로 설정.
경사하강법의 몸체인 for 반복문 구현하기.
lr = 0.8
# 1. 오차 함수를 random_tensor로 미분해야하기 때문에 `requires_grad`를 True로 설정한다.
for i in range(20000):
random_tensor.requires_grad_(True)
# 2. 랜덤 텐서를 `weird_function()`에 통과시켜 가설을 구하고,
# `distance_loss()` 함수에 가설과 오염된 이미지를 입력해 오차를 계산한다.
# 그 후, `loss.backward()` 함수를 호출하여 loss를 random_tensor로 미분한다.
hypoth = weird_function(random_tensor)
loss = distance_loss(hypoth, broken_image)
loss.backward()
# 3. 직접 경사하강법을 구현하기 위해 torch.no_grad() 함수를 이용해서
# 자동 기울기 계산 비활성화.
with torch.no_grad():
# 4. random_tensor.grad 에는 loss.backward() 함수에서 계산한 loss 의 기울기가 들어있음.
# 이 방향의 반대쪽으로 random_tensor를 학습률(lr)만큼 이동.
random_tensor = random_tensor - lr * random_tensor.grad
# 반복문 1000번 마다 오차 출력
if i % 1000 == 0:
print(f"loss at {i} = {loss.item()}")
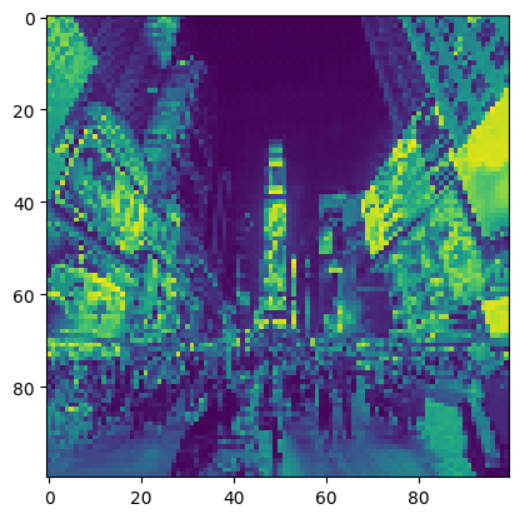
# random_tensor 가 제대로 복원되었는지 확인
plt.imshow(random_tensor.view(100, 100).data)
출력값
loss at 0 = 12.388728141784668
loss at 1000 = 1.1533136367797852
loss at 2000 = 0.5374141335487366
loss at 3000 = 0.3740074932575226
loss at 4000 = 0.29787084460258484
loss at 5000 = 0.25086307525634766
loss at 6000 = 0.21650207042694092
loss at 7000 = 0.18881291151046753
loss at 8000 = 0.1651799976825714
loss at 9000 = 0.14424003660678864
loss at 10000 = 0.12517927587032318
loss at 11000 = 0.10746888816356659
loss at 12000 = 0.09074938297271729
loss at 13000 = 0.07477107644081116
loss at 14000 = 0.05935865640640259
loss at 15000 = 0.04438850283622742
loss at 16000 = 0.02977452427148819
loss at 17000 = 0.021152310073375702
loss at 18000 = 0.021165795624256134
loss at 19000 = 0.021167615428566933
💡 해당 포스팅은 펭귄브로의 3분 딥러닝, 파이토치맛 교재를 통해 학습한 내용을 정리한 글입니다.